James Hansen’s recent paper uses detailed temperature records to demonstrate that the chance of an area experiencing extremely hot summer weather has increased dramatically in recent years. Several similar publications have shown recently how climate change has increased the likelihood of very adverse weather. Scientists like Hansen do this work because they are wrestling with the need to communicate to the general public that global temperatures won’t increase every year but that the chance of extreme events in the form of ferocious heat or catastrophic rainfall is rising rapidly. Hansen’s conclusions are important in that they are the first attempt to show how the frequency of very high land temperatures has risen. But the second major finding of his paper has not been noted by the scientific press: temperature variability has increased. Not only has the average temperature risen but the distribution of temperature has widened, meaning that extremes are more likely. We didn’t know this, and the finding is deeply worrying.

The ‘bell curve’

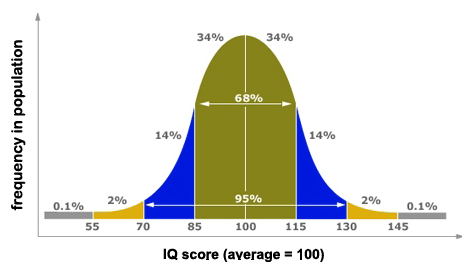
Many natural phenomena demonstrate a pattern called the ‘normal distribution’ or ‘bell curve’. Measure the height of Finnish women or the IQ of Singaporean children and the results will follow a predictable form that resembles the shape of a bell. Most observations are clustered around the mean with increasingly small numbers of results away from the central peak.

Temperatures follow this pattern. If I logged the average noon temperature for August days in London each year, I would find that the observations followed a bell curve pattern. Findings would be grouped around a central (mean) figure. The number of years above this level would be approximately equal to the numbers below it. The shape of the observations would be roughly symmetrical above and below the mean.

The bell curve is reassuringly familiar. In fact, it seems to me that humankind naturally assumes that most natural phenomena follow this pattern. This ‘normal distribution’ follows a clear statistical pattern. A calculation called the standard deviation predicts the width of the curve. Some distributions are quite tight, meaning that the curve has a small standard deviation and the curve falls sharply away from the mean. Others are fatter, with a high standard deviation. Whatever the size of the standard deviation, a proper bell curve has about 68% of all observations within one deviation of the mean. This percentage is almost universal.

Hansen’s paper calculates the standard deviation of summer temperatures (June-July- August) over land in the northern hemisphere. He shows the standard deviation was about 0.5 degrees C in the period 1950-1980. This number tells us that about 68% of all average 24 hour temperatures over the three month period for a particular spot will fall within the range +0.5 degrees to -0.5 degrees of the average. So if London’s average (24 hour) temperature is 16 degrees in the summer, it will be within the range 15.5 to 16.5 degreees just over two thirds of all years. This is quite a tight curve. Extreme variations of, say, +2.0 degrees are therefore very rare indeed.

Most models assume that the impact of climate change will be to shift the bell curve upwards. So if land temperatures rise by an average of 1 degree C, then London’s summer warmth will also rise by 1 degree, and the standard deviation will stay the same. One standard deviation (68% of observations are within this figure) will remain 0.5 degrees C. This is a convenient assumption: it implies that the effects of climate change are predictable and smooth. All that happens as the world warms is that the curve of likely future summer temperatures rises but the shape of the curve remains the same.

Hansen and his colleagues show that this is probably an incorrect assumption. They demonstrate that the curves of temperature are widening. The mean temperature is rising but the probability of extremely warm periods is increasing as well. The change isn’t massive. Hansen says that for the average spot in the northern hemisphere the standard deviation was 0.5 degrees in the period 1950 to 1980 but had risen to 0.54 or so in the period 1981 to 2010.

Also, the curve of possible outcomes is no longer symmetrical. Assessed against the average, the chance of very warm summers has increased sharply but the likelihood of colder summers has risen much less. (This means that the curve of temperatures doesn’t resemble a true bell curve any more – there’s a bulge on the higher side). All-in-all, the chance of really hot summers has increased quite sharply, even when assessed against a rising average global temperature. Global warming is significantly raising the chance of really extreme hot periods.

Until now, most climate scientists have assumed that bell curve will stay in shape. If Hansen’s research is correct and rising greenhouse gas concentration are producing a sharper increase in extreme hot events than predicted, we have yet another reason to worry. Adapting to a changing climate is more difficult if the extremes of hot weather or major rainfalls are more severe. (As we see in the American corn belt or the rain-hit north-west of England this summer.)

Even more fundamentally, some scientists have wondered whether the earth’s response to rising greenhouse gas concentrations would follow a bell curve type pattern or not. A doubling of pre-industrial greenhouse gas concentrations, which seems an increasingly likely outcome by 2050, was predicted to increase temperatures by between 2 degrees and 4.5 degrees with probability distributions within this range that resemble a traditional bell curve. Marty Weitzman at Harvard has led the questioning of whether this is a reasonable assumption. He suggests that the right hand side of the probability curve may be much ‘fatter’ than the left (and therefore resembling what is known as a Pareto distribution rather than a normal curve - think of the shape of a beached whale). Hansen’s latest gloomy paper gives some important support to Weitzman’s hypothesis of the fat rightward tail.

This may seem abstruse and academic statistical worrying. It is not. Humans are brought up to expect the normal distribution in natural phenomena. Measure the height of your colleagues at work, or the time they take to drink a cup of coffee and you will find an approximately standard bell curve. We have instinctively assumed that temperature changes will continue to exhibit the same probability distribution as they have in the past. Remove that comfortable assumption and we have another major uncertainty to worry about.